Using image processing, we were taught to estimate an area desired using Green's Function. Green's function, as you know, relates a double integral to a line integral. This is very handy because by just traversing a line, we can be able to know the area enclosed by that line. Well, must have an enclosed line..
Numerically, the discreet form of the Green's theorem in obtaining the data, is like this:
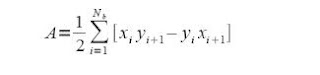 where Nb is the number of pixels in the line or contour.
where Nb is the number of pixels in the line or contour.We first used different shapes. Shapes used were rectangle, triangle and a circle. We applied the Green's theorem in those shapes and then we compare the obtained area with the theoretical area.
Shape #1: Rectangle.
The rectangle used is a 400x400 pixel rectangle. Using the Green's function, it has obtained an area of 49170 pixels. Amazingly, the theorectical was 49170 pixels too. The picture and the code is shown below.
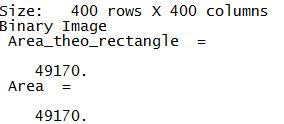
Result.
 Code for rectangle.
Code for rectangle.
 Code for rectangle.
Code for rectangle.#note: If you notice, there is a line after the for loop that says A1(Nb). Because the limit of the for loop is until Nb-1, We have to show the value at Nb. Since we need the contour to be continous, Nb+1 = 1.
#note: Theoretical Area is obtained by finding the max and min of x and y, to find the length in pixels. Area is then a simple L x W.
For Triangle, the code is almost the same except for the theoretical area that is 0.5* B * H.

Code for Green's function in Triangle.

Image of the Quezon City Circle thanks to Google Maps. :)
#note: Theoretical Area is obtained by finding the max and min of x and y, to find the length in pixels. Area is then a simple L x W.
For Triangle, the code is almost the same except for the theoretical area that is 0.5* B * H.

Code for Green's function in Triangle.

Image of the Quezon City Circle thanks to Google Maps. :)
First, aim is to obtain a black and white image of the contour of the QC circle like the previous shapes. What i did is that I highlighted the desired area white for i to have a constant value like this:

And then I used im2gray() and im2bw() to obtain a threshold for me to have a black and white image of the contour. It yielded this:

This is used in the Green's function program.
The code to obtain the Area using Green's function is shown below:
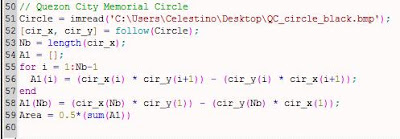
The Area obtained using this code is:
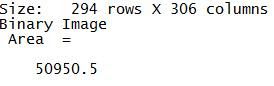 In order to get the Theoretical Area, I noted the coordinates of the end points of the two ds(D1 and d2). Since it is an ellipse, there is a need for two rs. (r1 and r2). By using the coordinates of the endpoints of the segments assumed as the diameter, the distance formula was used which obtained d1 = 287 and d2 = 213. Dividing them by half, we'll find r1 and r2 chich is 143.5 and 106.5 respectively. with this we can use the equation of an ellipse which is A = pi * r1*r2.
In order to get the Theoretical Area, I noted the coordinates of the end points of the two ds(D1 and d2). Since it is an ellipse, there is a need for two rs. (r1 and r2). By using the coordinates of the endpoints of the segments assumed as the diameter, the distance formula was used which obtained d1 = 287 and d2 = 213. Dividing them by half, we'll find r1 and r2 chich is 143.5 and 106.5 respectively. with this we can use the equation of an ellipse which is A = pi * r1*r2.
Theoretical Area yielded 47987.835 pixels. This is close to 50950 pixels. This is a 6% decviation from the theoretical. By the scale in google maps, it is found out that for every 200m, there is 87 pixel length. so, Total Area in meters will be 47987.835p * 200m/87p *200m/87p = 253121 square meters.
I think in this activity , I'd get an 9 out of 10. Because, I am able to do everything that is said. I got trouble checking the accuracy of my desired landmark due to software constraints.

And then I used im2gray() and im2bw() to obtain a threshold for me to have a black and white image of the contour. It yielded this:

This is used in the Green's function program.
The code to obtain the Area using Green's function is shown below:

The Area obtained using this code is:
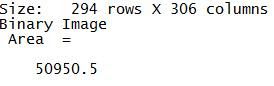 In order to get the Theoretical Area, I noted the coordinates of the end points of the two ds(D1 and d2). Since it is an ellipse, there is a need for two rs. (r1 and r2). By using the coordinates of the endpoints of the segments assumed as the diameter, the distance formula was used which obtained d1 = 287 and d2 = 213. Dividing them by half, we'll find r1 and r2 chich is 143.5 and 106.5 respectively. with this we can use the equation of an ellipse which is A = pi * r1*r2.
In order to get the Theoretical Area, I noted the coordinates of the end points of the two ds(D1 and d2). Since it is an ellipse, there is a need for two rs. (r1 and r2). By using the coordinates of the endpoints of the segments assumed as the diameter, the distance formula was used which obtained d1 = 287 and d2 = 213. Dividing them by half, we'll find r1 and r2 chich is 143.5 and 106.5 respectively. with this we can use the equation of an ellipse which is A = pi * r1*r2.Theoretical Area yielded 47987.835 pixels. This is close to 50950 pixels. This is a 6% decviation from the theoretical. By the scale in google maps, it is found out that for every 200m, there is 87 pixel length. so, Total Area in meters will be 47987.835p * 200m/87p *200m/87p = 253121 square meters.
I think in this activity , I'd get an 9 out of 10. Because, I am able to do everything that is said. I got trouble checking the accuracy of my desired landmark due to software constraints.


.png)


















